揭秘：log对数的基本公式是什么？

探索数学奥秘：揭秘log对数基本公式

在数学的浩瀚宇宙中，隐藏着无数令人着迷的规律和公式。它们如同璀璨的星辰，引领着我们探索未知的世界。今天，我们要揭开一个极具魅力的数学工具——log对数的基本公式的神秘面纱。它不仅是数学分析中的基础，更是计算机科学、物理学、化学等多个领域不可或缺的工具。

一、初识log对数

首先，让我们来了解一下log对数的基本概念。对数（logarithm）是幂运算（exponentiation）的逆运算。简单来说，如果a^x = N（a > 0，且a ≠ 1），那么x就是N以a为底的对数，记作x = log_a N。这里，a被称为对数的底数，N被称为真数，x则是对数的值。

二、log对数的基本公式

1. 对数的定义式

我们已经提到了对数的定义式：x = log_a N ⇔ a^x = N。这是log对数最基本的公式，它建立了指数与对数之间的桥梁。通过这个公式，我们可以将指数运算转化为对数运算，反之亦然。

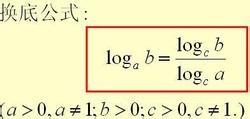
2. 对数的换底公式

在数学中，我们经常需要计算不同底数的对数。幸运的是，我们有一个非常实用的工具——对数的换底公式：log_b a = log_c a / log_c b（c > 0，c ≠ 1）。这个公式允许我们将一个底数的对数转换为另一个底数的对数，极大地简化了计算过程。

3. 对数的运算法则

对数的运算法则是解决复杂对数问题的关键。它们包括：

和差法则：log_a (M × N) = log_a M + log_a N

商法则：log_a (M / N) = log_a M - log_a N

幂法则：log_a (M^n) = n × log_a M

这些法则使得我们可以将复杂的对数表达式简化为更简单的形式，从而更容易进行计算。

三、log对数的应用

1. 简化计算

对数的一个显著应用是简化计算。在计算器发明之前，人们需要依靠对数表来进行复杂的乘法、除法运算。通过对数运算，我们可以将乘法、除法转化为加法、减法，从而大大提高了计算效率。

2. 解决实际问题

对数在解决实际问题中发挥着重要作用。例如，在物理学中，我们经常需要处理指数衰减或增长的问题，对数可以帮助我们更直观地理解这些现象。在化学中，pH值是一个以对数为基础的重要指标，它反映了溶液的酸碱度。在金融领域，复利计算也涉及到了对数运算。

3. 数据分析与可视化

在数据分析领域，对数变换是一种常用的数据预处理技术。通过对数据进行对数变换，我们可以缩小数据的范围，使得数据更加易于处理和分析。此外，对数变换还可以帮助我们揭示数据中的隐藏模式，提高数据可视化的效果。

4. 机器学习中的对数损失函数

在机器学习中，对数损失函数（如交叉熵损失）是评估模型性能的重要指标。这些损失函数基于对数运算，能够反映模型预测值与真实值之间的差异。通过最小化这些损失函数，我们可以优化模型的参数，提高模型的预测能力。

四、log对数的数学之美

log对数不仅具有实用价值，还蕴含着丰富的数学之美。它揭示了指数与对数之间的对称关系，使得我们可以从另一个角度审视数学世界。此外，对数还与欧拉数e、圆周率π等数学常数紧密相连，共同构成了数学中一道亮丽的风景线。

五、探索log对数的深度与广度

尽管我们已经了解了log对数的基本公式和应用，但数学的世界是无穷无尽的。随着我们对log对数的深入研究，我们会发现更多关于它的奥秘和美妙之处。例如，我们可以探索对数的性质、对数函数的图像和性质、对数不等式等高级话题。此外，我们还可以将log对数与其他数学分支相结合，如微积分、概率论等，从而拓展我们的数学视野。

六、结语

通过本文的介绍，我们了解了log对数的基本公式、应用以及它所蕴含的数学之美。log对数不仅是数学分析中的基础工具，更是多个领域不可或缺的数学语言。它让我们能够更深入地理解世界，解决复杂问题。希望这篇文章能够激发你对log对数的兴趣，引领你走向更广阔的数学天地。在未来的日子里，让我们一起继续探索数学的奥秘，感受数学带来的无穷魅力吧！